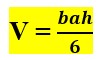Tema No. 2
Tema No. 2
Volumen del prisma rectangular y la pirámide triangular
v
Prisma
rectangular
El volumen de un prisma
rectangular se calcula como el producto de sus dimensiones
(las aristas a, b y h).
Un prisma rectangular (u ortoedro) es un poliedro cuya superficie está formada por dos rectángulos iguales y paralelos llamados bases y por cuatro caras laterales que son
también rectángulos paralelos e iguales dos a dos.
Siendo a y b los
lados diferentes de las bases y h la
altura.
El volumen del prisma es
el producto del área de la base (Ab) por la altura (h).
En este caso, la base es un rectángulo, por lo
que su área es el producto de los dos lados contiguos (a·b).
Ejemplo:
Sea
un prisma rectangular de
dimensiones conocidas, siendo los lados contiguos de la base a = 3 cm
y b = 1,5 cm y la altura h = 4 cm. ¿Cuál es el volumen?
v Pirámide triangular
El
volumen de una pirámide triangular es igual al espacio tridimensional ocupado
por la pirámide. El volumen de cualquier pirámide es igual
al área de la base por la altura de la pirámide dividido por tres.
A su vez, sabemos que la base de una
pirámide triangular es un triángulo y el área de cualquier triángulo es
encontrada al multiplicar a la longitud de su base por su altura y dividir por
dos. Entonces, tenemos:
en donde, b es la
longitud de la base del triángulo, a es la longitud de
la altura del triángulo y h es la altura de la
pirámide.
Ejemplo:
Una pirámide tiene una altura de 5 m, y una
base triangular con base de longitud 4 m y altura de 3 m. ¿Cuál es su volumen?
Datos
·
Altura de la pirámide, h = 5 m
·
Base del triángulo, b = 4 m
·
Altura del triángulo, a = 3 m
Usamos
esto valores en la fórmula del volumen:
Taller Sumativo No. 2
Volumen del prisma rectangular y la pirámide triangular
INDICACIONES GENERALES
·
Desarrolle en forma ordenada en su
cuaderno de matemática el Taller Sumativo No. 2. Colóquele nombre y grupo con
bolígrafo en cada una de las páginas antes de tomar las fotos. NO se aceptan talleres con el nombre escrito
con editor de textos.
·
Resuelva
en forma ordenada.
·
A
cada problema le debe colocar el procedimiento, ya que estos forman parte de la evaluación.
·
Al
resolver la asignación ejerza la presión necesaria con el lápiz sobre el
papel de tal forma que, al tomar la fotografía de la asignación, no se
dificulte la verificación de las respuestas.
·
Tómele
fotografía a lo que desarrolló en su cuaderno.
Cada fotografía debe tener nombre y grupo escrito con
bolígrafo. Debe asegurarse que en las
fotografías esté visible todo lo que desarrolló en su cuaderno.
·
Las
fotografías en que se dificulte la revisión del Taller Sumativo serán devueltas
hasta que se hagan las correcciones.
·
Las
fotografías las debe enviar al correo julio.rios20@meduca.edu.pa
En Asunto le debe
colocar: Taller Sumativo No. 2
·
Fecha
de entrega: desde el
martes 21 hasta las 12:30
m.d. del lunes 27 de septiembre.
·
Pasada
la fecha y hora asignada para la entrega del taller, ya NO SERÁ RECIBIDO.
Nombre:
____________________________ Grupo: 9° _____ Valor: 30 puntos
Fecha de entrega: desde el martes 21 hasta las 12:30 m.d. del lunes 27 de septiembre.
Profesor: Julio Ríos R.
Calcule el volumen (V) de los prismas rectangulares y de las pirámides
triangulares. Debe colocar todos los
procedimientos paso a paso, incluyendo los datos, tal cual aparece explicado en
cada uno de los ejemplos. Los
procedimientos forman parte de la evaluación, debe colocarlos.
v
Prisma
rectangular
v Pirámide triangular
a) ¿Cuál es el volumen de una pirámide que
tiene una altura de 8 m, y una base triangular de base de 5 m y altura de 6 m?
b) ¿Cuál es el volumen de una pirámide que tiene una altura
de 10 dm, y una base triangular con base de longitud 7 dm y altura de 6 dm?
c)
¿Cuál es el volumen de una
pirámide que tiene una altura de 12 cm, y una base triangular con base de
longitud 8 cm y altura de 9 cm?
